2. Векторы
3. Стереометрия
4. Начала теории вероятностей
6. Простейшие уравнения
7. Преобразование выражений
8. Производная функции
9. Практические задачи
10. Текствые задачи
11. Графики функций
12. Исследование функций
13. Уравнения
14. Стереометрия с доказ-вом
15. Неравенства
16. Финансовая математика
17. Планиметрия с доказ-вом
18. Задачи с параметром
19. Задачи на логику
БАЗА ЗАДАНИЙ
Задание № 3. Стереометрия.
1. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
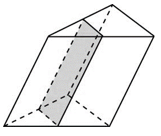
Ответ: 16
2. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Ответ: 8
3. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?
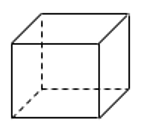
Ответ: 9
4. Площадь поверхности куба равна 24. Найдите его объем.
Ответ: 8
5. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 30. Найдите ребро куба.
Ответ: 2
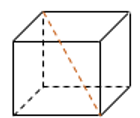
6. Площадь поверхности куба равна 8. Найдите его диагональ.
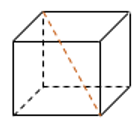
Ответ: 2
7. Объем куба равен 24√3. Найдите его диагональ.
Ответ: 6
8. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Ответ: 4
9. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4. Площадь ее поверхности равна 132. Найдите высоту призмы.
Ответ: 10
10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Ответ: 120
11. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
Ответ: 12
12. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.
Ответ: 248
13. В основании прямой призмы лежит ромб с диагоналями, равными 9 и 12. Площадь ее поверхности равна 468. Найдите боковое ребро этой призмы.
Ответ: 12
14. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.
Ответ: 22
15. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Ответ: 6
16. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
Ответ: 7
17. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Ответ:32
18. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.
Ответ: 3
19. Диагональ прямоугольного параллелепипеда равна √8 и образует углы 30°,30° и 45° с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.
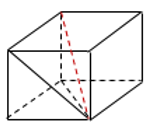
Ответ: 4
20. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1=32, AB=12, AD=9. Найдите площадь сечения проходящее через вершины A, A1, C.
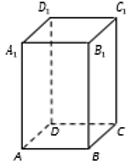
Ответ: 480
21. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1=16, А1B1=2, A1D1=8. Найдите длину диагонали AC1.
Ответ: 18
22. Дана правильная четырёхугольная призма ABCDA1B1C1D1, площадь основания которой равна 6, а боковое ребро равно 7. Найдите объём многогранника, вершинами которого являются точки A, B, C, B1.
Ответ: 7
23. Найдите объём многогранника, вершинами которого являются точки C, A1, B1 , C1 правильной треугольной призмы ABCA1B1C1 , площадь основания которой равна 4, а боковое ребро равно 9.
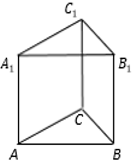
Ответ: 12
24. Найдите объём многогранника, вершинами которого являются точки A, C, A1, B1, C1 правильной треугольной призмы ABCA1B1C1. Площадь основания призмы равна 7, а боковое ребро равно 9.
Ответ: 42
25. В правильной треугольной призме ABCA1B1C1 все ребра равны 3. Найдите угол между прямыми AA1и BC1. Ответ дайте в градусах.
Ответ: 45°
26. В правильной треугольной призме ABCA1B1C1 известно, что AB=√3AA1. Найдите угол между прямыми AB1 и CC1. Ответ дайте в градусах.
Ответ: 60°
27. Объём куба равен 16. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
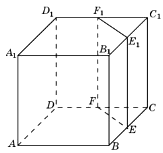
Ответ: 2
28. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
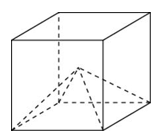
Ответ: 2
29. Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объем треугольной пирамиды AD1CB1.
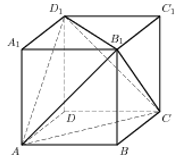
Ответ: 1,5
30. Объем параллелепипеда ABCDA1B1C1D1 равен 1,5. Найдите объем треугольной пирамиды ABCB1.
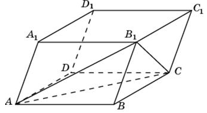
Ответ: 0,25
31. Найдите объем параллелепипеда ABCDA1B1C1D1, если объем треугольной пирамиды ABDA1 равен 3.
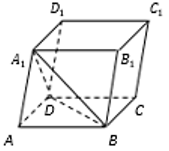
Ответ: 18
32. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол 60° и равно 2. Найдите объем параллелепипеда.
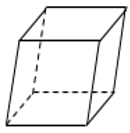
Ответ: 1,5
33. Найдите объём многогранника ACDFA1C1D1F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 9, а боковое ребро равно 11.
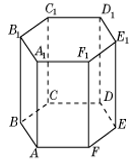
Ответ: 66
34. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки A до прямой E1D1.
Ответ: 14
35. Найдите объём многогранника DA1B1C1D1E1F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 2.
Ответ: 8
36. Найдите объём многогранника CDEC1D1E1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 14.
Ответ:14
37. Найдите объём многогранника A1B1F1A правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 15.
Ответ: 10
38. В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.
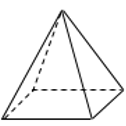
Ответ: 28
39. В правильной четырёхугольной пирамиде боковое ребро равно 7,5, а сторона основания равна 10. Найдите высоту пирамиды.
Ответ: 2,5
40. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Ответ: 96
41. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
Ответ: 13
42. В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды.
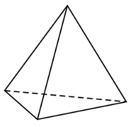
Ответ: 3,5