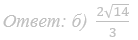2. Векторы
3. Стереометрия
4. Начала теории вероятностей
6. Простейшие уравнения
7. Преобразование выражений
8. Производная функции
9. Практические задачи
10. Текствые задачи
11. Графики функций
12. Исследование функций
13. Уравнения
14. Стереометрия с доказ-вом
15. Неравенства
16. Финансовая математика
17. Планиметрия с доказ-вом
18. Задачи с параметром
19. Задачи на логику
БАЗА ЗАДАНИЙ
Задание № 14. Стереометрия с доказательством.
49. В одном основании прямого кругового цилиндра с высотой 3 и радиусом основания 8 проведена хорда AB, равная радиусу основания, а в другом его основании проведён диаметр CD, перпендикулярный AB. Построено сечение ABNM, проходящее через прямую AB перпендикулярно прямой CD так, что точка C и центр основания цилиндра, в котором проведён диаметр CD, лежат с одной стороны от сечения.
а) Докажите, что диагонали этого сечения равны между собой.
б) Найдите объём пирамиды CABNM.
Ответ: б) 64+32√3
50. В кубе ABCDA1B1C1D1 все ребра равны 6.
а) Докажите, что угол между прямыми АС и BD1 равен 60°.
б) Найдите расстояние между прямыми АС и BD1.
Ответ: б) 2√3
51. В правильной треугольной призме ABCA1B1C1 все рёбра равны 2. Точка M — середина ребра AA1.
а) Докажите, что прямые MB и B1C перпендикулярны.
б) Найдите расстояние между прямыми MB и B1C.
Ответ: б) √30/5
52. В правильной четырёхугольной пирамиде PABCD сторона основания ABCD равна 12, боковое ребро PA ―12√2. Через вершину A проведена плоскость a, перпендикулярная прямой PC и пересекающая ребро PC в точке K.
а) Докажите, что плоскость a делит высоту PH пирамиды PABCD в отношении 2:1, считая от вершины P.
б) Найдите расстояние между прямыми PH и BK.
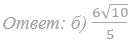
53. Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре AA1 отмечена точка K так, что AK: KA1 = 1 : 2. Плоскость a проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD1 в точке M.
а) Докажите, что MD:MD1=2:1.
б) Найдите площадь сечения, если AB=4, AA1=6.
Ответ: б) 8√6
54. На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ:OB=1:2. Точка P — середина ребра AS.
а) Докажите, что плоскость DPQ перпендикулярна плоскости основания пирамиды.
б) Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.
Ответ: б) √5
55. В правильном тетраэдре АВС точка Н — центр грани АВС, а точка М — середина ребра СD.
а) Докажите, что прямые АВ и СD перпендикулярны.
б) Найдите угол между прямыми DН и ВМ.
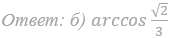
56. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C1, причём CC1 — образующая цилиндра, а AC — диаметр основания. Известно, что ∠ACB=30°, AB=√2, CC1=2.
а) Докажите, что угол между прямыми AC1 и BC равен 45°.
б) Найдите объём цилиндра.
Ответ: б) 4π
57. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки B1 и C1, причем BB1 — образующая цилиндра, а отрезок AC1 пересекает ось цилиндра.
а) Докажите, что угол ABC1 прямой.
б) Найдите угол между прямыми BB1 и AC1, если АВ = 6, BB1=15, B1C1=8.
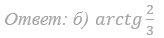
58. В основании прямой треугольной призмы ABCA1B1C1 . лежит равнобедренный (AB = BC) треугольник ABC. Точки K и M — середины рёбер A1B1 и AC соответственно.
а) Докажите, что KM = KB.
б) Найдите угол между прямой KM и плоскостью ABB1, если AB = 8, AC = 6 и AA1= 3.
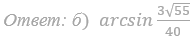
59. Дана правильная треугольная призма ABCA1B1C1 , у которой сторон основания равна 2, а боковое ребро равно 3. Через точки A, C1 и середину T ребра A1B1 проведена плоскость.
а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.
б) Найдите угол между плоскостью сечения и плоскостью ABC.
Ответ: б) arctg 3
60. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 стороны основания равны 4, а боковые ребра 5.
а) Докажите, что плоскость A1C1E перпендикулярна плоскости BB1E1.
б) Найдите угол между плоскостями A1C1E и ABC.
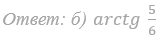
61. В треугольной пирамиде SABC основанием является правильный треугольник ABC, а ребро SB перпендикулярно плоскости основания. Точки D, E и F середины ребер AB, BC и BS соответственно.
а) Докажите, что плоскость DEF делит пополам высоту пирамиды, проведенную из вершины B.
б) Найдите расстояние от точки B до плоскости DEF, если AB=6, AS=10.
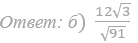
62. В основании пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=4 и BC=√33, все боковые ребра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка Е, а на ребре AS отмечена точка F так, что SF=BE=3.
а) Докажите, что плоскость CEF параллельна SB.
б) Пусть плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от Q до плоскости АВС.
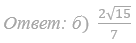
63. Дана правильная четырехугольная пирамида MABCD, все ребра которой равны 12. Точка N – середина бокового ребра MA, точка K делит боковое ребро MB в отношении 2:1, считая от вершины M.
а) Докажите, что сечение пирамиды плоскостью, проходящей через точки N и K параллельно прямой AD, является равнобедренной трапецией.
б) Найдите площадь этого сечения.
Ответ: б) 7√51
64. На окружности основания конуса с вершиной S отмечены точки A, B и C так, что AB=BC. Медиана AM треугольника ASC пересекает высоту конуса.
а) Точка N - середина отрезка AC. Докажите, что угол MNB прямой.
б) Найдите угол между прямыми AM и SB, если AS=2, AC=√6.

65. В основании правильной пирамиды PABCD лежит квадрат ABCD со стороной 6. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды.
Ответ: б) 12√3
66. В правильной треугольной пирамиде SABC с основанием ABC боковое ребро равно 5, а сторона основания равна 4. На продолжении ребра SA за точку A отмечена точка P, а на продолжении ребра SB за точку B —точка Q, причём AP= BQ = SA.
а) Докажите, что прямые PQ и SC перпендикулярны друг другу.
б) Найдите угол между плоскостями ABC и CPQ.
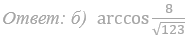
67. Плоскость α проходит через середину ребра AD прямоугольного параллелепипеда ABCDA1B1C1D1 . перпендикулярно прямой BD1.
а) Докажите, что угол между плоскостью α и плоскостью ABC равен углу между прямыми BB1 и B1D.
б) Найдите угол между плоскостью α и плоскостью ABC, если объём параллелепипеда ABCDA1B1C1D1 равен 48√3, AB = 2√3 и AD = 6.
Ответ: б) 60°
68. На ребре AA1прямоугольного параллелепипеда ABCDA1B1C1D1 взята точка Е так, что A1E=6AE. Точка Т - середина ребра B1C1. Известно, что АВ =4√2, AD=12, AA1=14.
a) Докажите, что плоскость ETD1 делит ребро BB1 в отношении 4:3.
б) Найдите площадь сечения параллелепипеда плоскостью ETD1.
Ответ: б) 90
69. Дана пирамида SABC в которой SC=SB=AB=AC=√17, SA=BC=2√5 .
а) Докажите, что ребро SA перпендикулярно ребру BC.
б) Найдите расстояние между ребрами BC и SA.
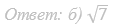
70. Дан куб ABCDA1B1C1D1 . Точка K – середина ребра C1D1.
а) Докажите, что расстояние от вершины A1 до прямой BK равно ребру куба.
б) Найдите угол между плоскостями KBA1 и BCC1.
Ответ: б) arccos 2/3
71. На продолжениях рёбер A1A и D1C1 прямоугольного параллелепипеда ABCDA1B1C1D1 отмечены точки K и L соответственное, причем AA1=AK, C1D1=C1L.
а) Докажите, что прямая KL проходит через середину ребра BC.
б) Найдите угол между прямыми AD1 и KL, если AB=2√2, AD=6, AA1=8.
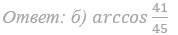
72. На ребре AB правильной треугольной пирамиды SABC с основанием ABCотмечена точка K, причём AK=15, BK=3. Через точку K проведена плоскость α, параллельная плоскости SBC.
а) Докажите, что плоскость α проходит через середину высоты пирамиды.
б) Найдите расстояние между плоскостями α и SBC, если высота пирамиды равна 13.
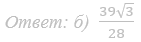
73. В правильной треугольной пирамиде SABC точка P – делит сторону AB в отношении 2:3 считая от вершины A, точка K – делит сторону BC в отношении 2:3 считая от вершины C. Через точки P и K параллельно SB проведена плоскость a.
а) Докажите, что сечение пирамиды плоскостью a является прямоугольником.
б) Найдите расстояние от точки S до плоскости a если известно, что SC=5, AC=6.
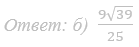
74. В правильной треугольной пирамиде SABC сторона основания AB=9, а боковое ребро SA=6. На ребрах AB и SC отмечены точки K и M соответственно, причем AK : KB=SM : MC =2:7. Плоскость a содержит прямую KM и параллельна прямой SA.
а) Докажите, что плоскость a делит ребро SB в отношении 2:7 считая от вершины S.
б) Найдите расстояние между прямыми SA и KM.
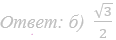
75. В правильной четырехугольной пирамиде SABCD сторона основания AB=3, абоковое ребро SA=6. Точка K делит ребро SC, причем SK:KC=1:2. Плоскость a проходит через точку K и параллельна SAD.
а) Докажите, что сечение пирамиды плоскость a является равнобедренной трапецией.
б) Найдите объем пирамиды, вершиной которой является точка S, а основание – сечение пирамиды SABC плоскость a.