банк заданий
Обсуждение заданий:
репетитор

Индивидуальная онлайн подготовка к ЕГЭ - 2025 по математике с профессиональным специалистом.
Легко, понятно, эффективно!
Тел.: 8-913-866-07-50 (Telegram, WhatsApp).
№8 производная функции
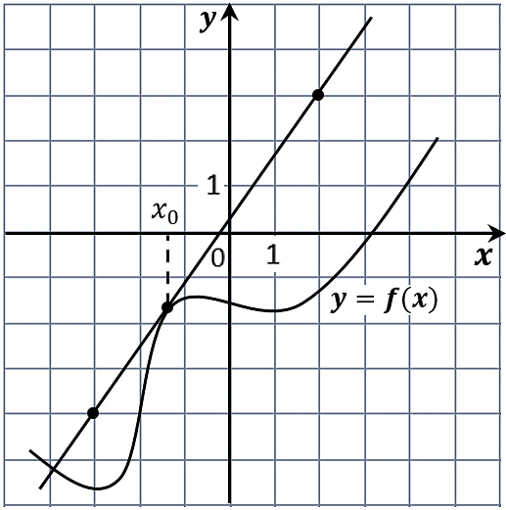
1. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: 1,4
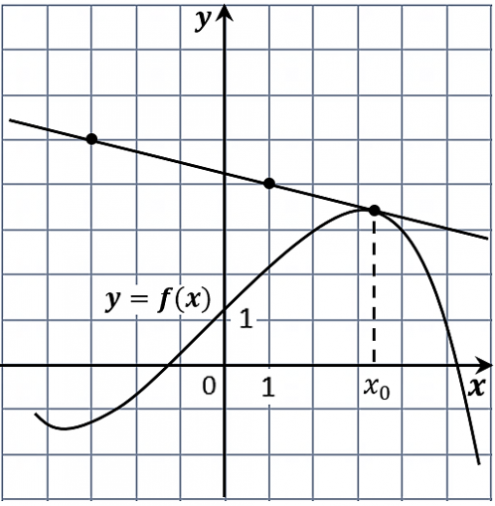
2. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ: -0,25
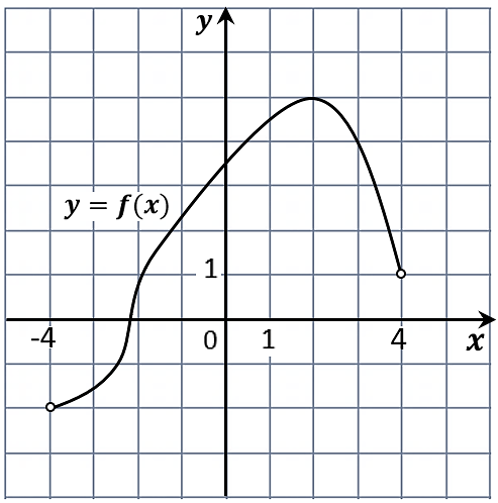
3. На рисунке изображён график функции y=f(x) , определённой на интервале (− 4; 4). Найдите корень уравнения f/(x) = 0 .
Ответ: 2
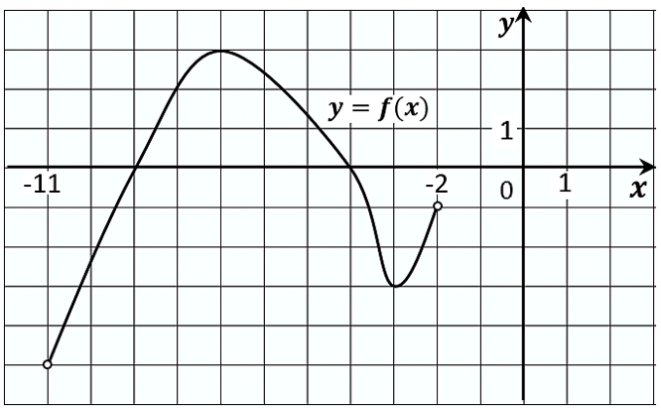
4. На рисунке изображён график дифференцируемой функции y=f(x), определённой на интервале (− 11; − 2). Найдите точку из отрезка [− 10; − 4], в которой производная функции f(x) равна 0.
Ответ: -7
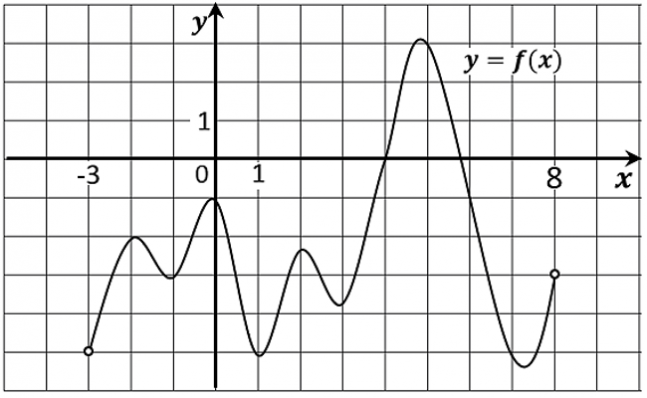
5. На рисунке изображён график функции y=f(x), определённой на интервале (− 3; 8). Найдите количество точек, принадлежащих отрезку [-2; 4], в которых производная функции f(x) равна 0.
Ответ: 6
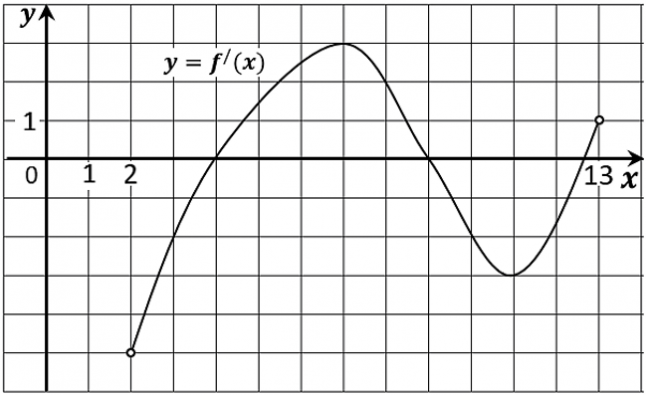
6. На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (2; 13). Найдите точку максимума функции f(x).
Ответ: 9
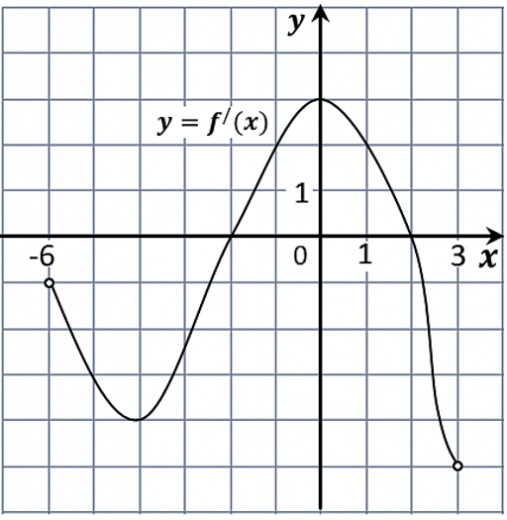
7. На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (− 6; 3). Найдите точку минимума функции f(x).
Ответ: -2
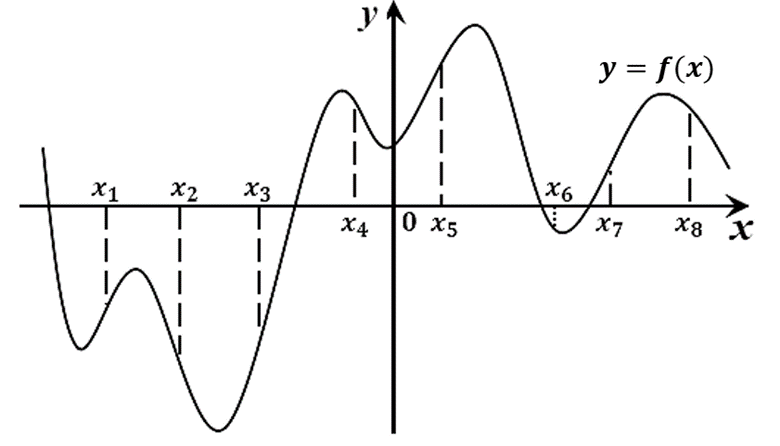
8. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) отрицательна?
Ответ: 4
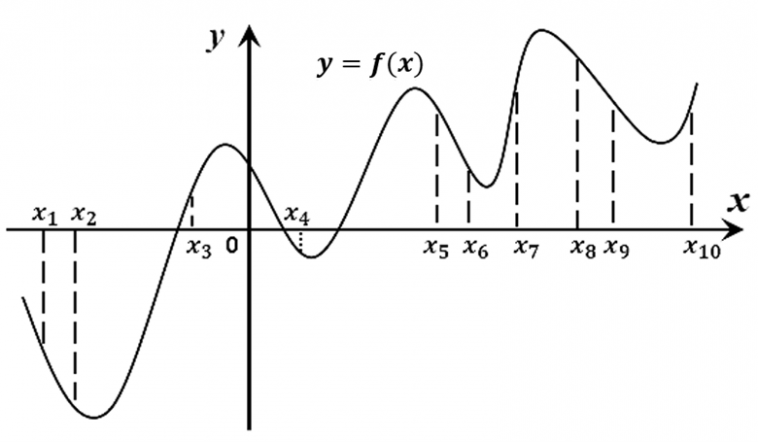
9. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены десять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. В скольких из этих точек производная функции f(x) положительна?
Ответ: 3
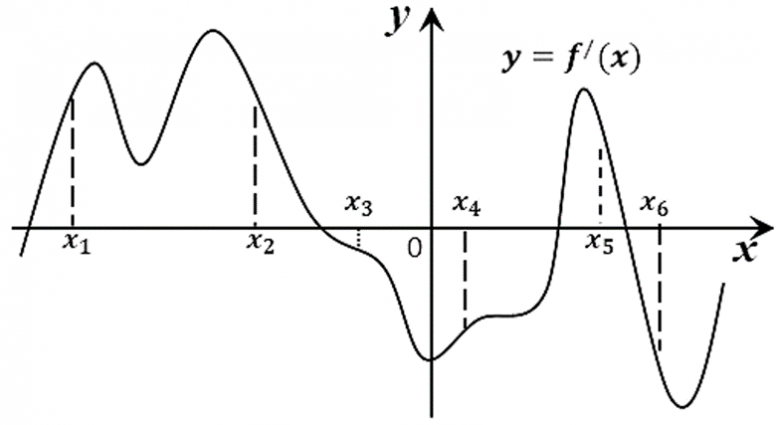
10. На рисунке изображён график y=f '(x) — производной функции f(x). На оси абсцисс отмечено шесть точек: x1, x2, x3, x4, x5, x6. Сколько из этих точек принадлежит промежуткам возрастания функции f(x)?
Ответ: 3
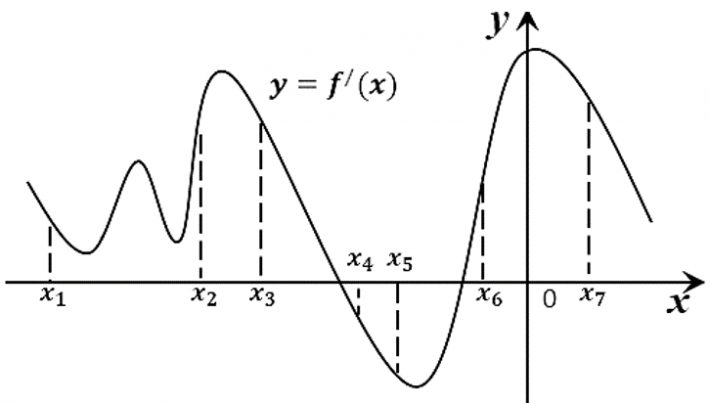
11. На рисунке изображён график y=f '(x) — производной функции f(x). На оси абсцисс отмечено семь точек: x1, x2, x3, x4, x5, x6, x7. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?
Ответ: 2
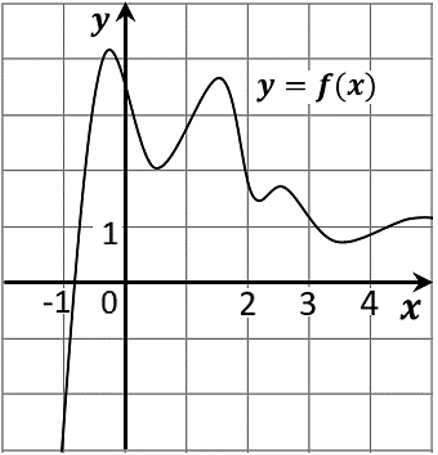
12. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки − 1, 2, 3, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Ответ: -1
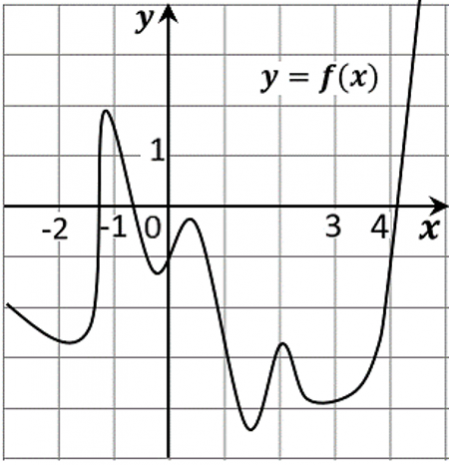
13. На рисунке изображён график функции y=f(x). На оси абсцисс отмечены точки − 2, − 1, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Ответ: -1
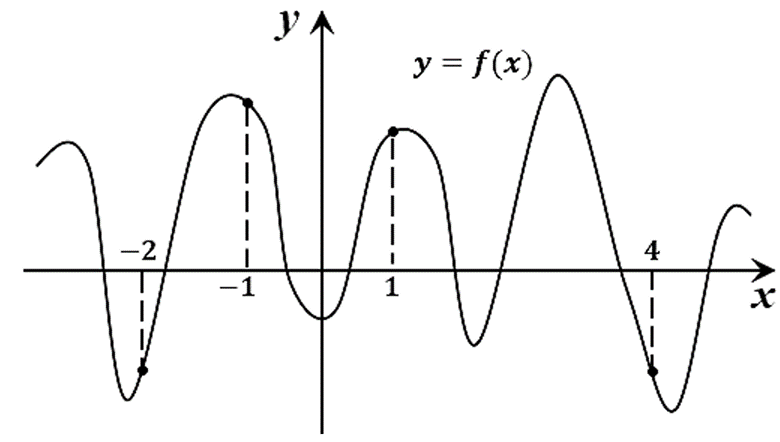
14. На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Ответ: 4
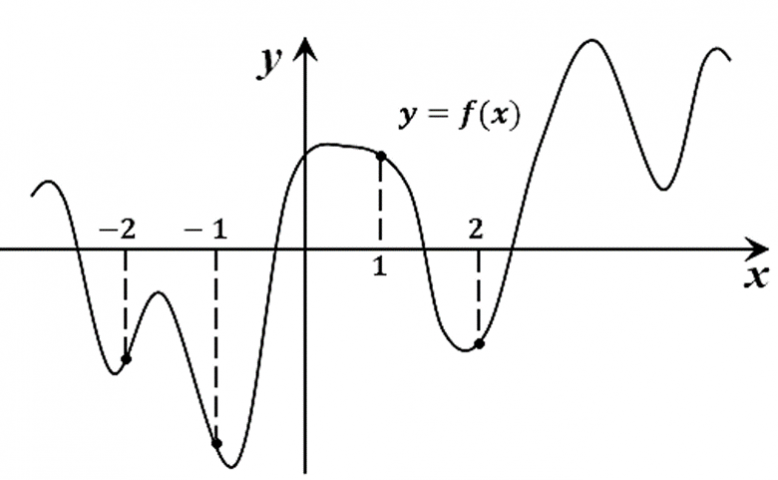
15. На рисунке изображен график функции y=f(x) и отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Ответ: -2
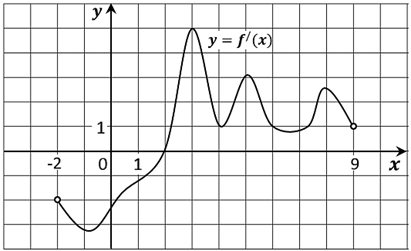
16. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 2; 9). В какой точке отрезка [2; 8] функция f(x) принимает наибольшее значение?
Ответ: 8
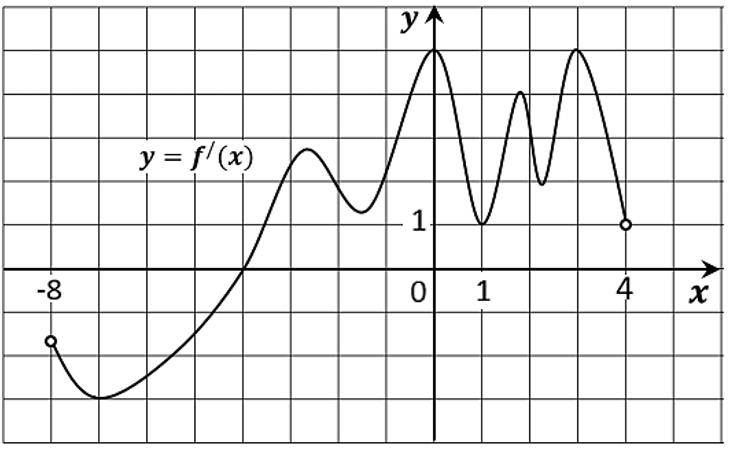
17. На рисунке изображён график y=f′(x) производной функции f(x), определённой на интервале (− 8; 4). В какой точке отрезка [− 2; 3] функция f(x) принимает наименьшее значение?
Ответ: -2
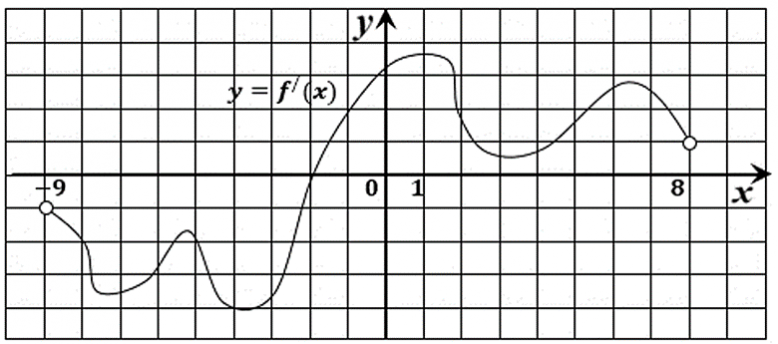
18. На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].
Ответ: -2
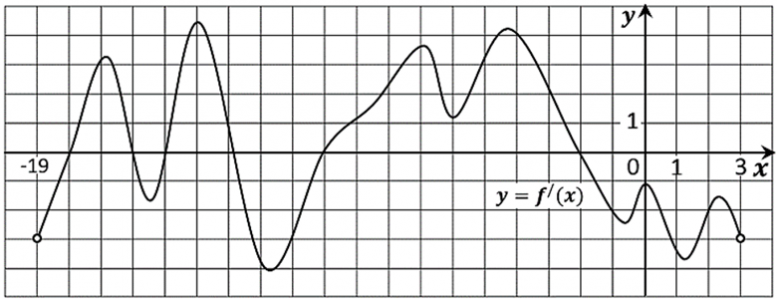
19. На рисунке изображен график y=f′(x) — производной функции f(x), определенной на интервале (-19; 3). Найдите количество точек экстремума функции f(x) на отрезке [-17; -4].
Ответ: 4
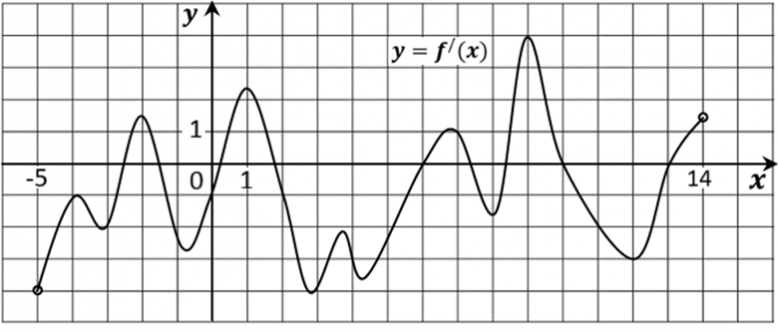
20. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 5; 14). Найдите количество точек минимума функции f(x), принадлежащих отрезку [− 4; 7].
Ответ: 3
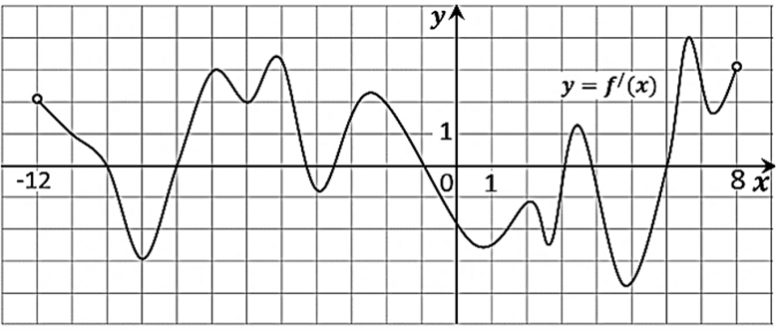
21. На рисунке изображён график y=f '(x) — производной функции f(x), определённой на интервале (− 12; 8). Найдите количество точек максимума функции f(x), принадлежащих отрезку [− 11; 5].
Ответ: 4