банк заданий
Обсуждение заданий:
репетитор

Индивидуальная онлайн подготовка к ЕГЭ - 2025 по математике с профессиональным специалистом.
Легко, понятно, эффективно!
Тел.: 8-913-866-07-50 (Telegram, WhatsApp).
№3 стереометрия
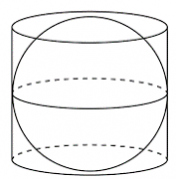
1. Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 30. Найдите площадь поверхности шара.
Ответ: 20

2. Шар вписан в цилиндр. Площадь поверхности шара равна 50. Найдите площадь полной поверхности цилиндра.
Ответ: 75

3. Шар вписан в цилиндр. Объем шара равен 18. Найдите объем цилиндра.
Ответ: 27

4. Цилиндр, объем которого равен 18, описан около шара. Найдите объем шара.
Ответ: 12
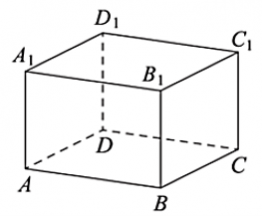
5. Найдите объем многогранника вершинами которого являются точки A, B, C, D, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=12, BC=4, BB1=7.
Ответ: 112

6. Найдите объем многогранника вершинами которого являются точки C, D, A1, B1, C1, D1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=2, BC=6, BB1=8.
Ответ: 48
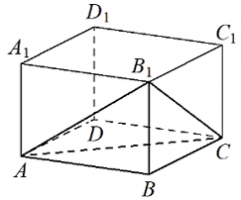
7. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, AB=9, BC=7, AA1=6. Найдите объём многогранника, вершинами которого являются точки A, B, C, B1.
Ответ: 63

8. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, AB=7, BC=6, AA1=5. Найдите объём многогранника, вершинами которого являются точки A, B, C, A1, B1, C1.
Ответ: 105

9. Найдите объём многогранника, вершинами которого являются точки A, D, C1, D1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=7, AD=3, AA1=8.
Ответ: 28
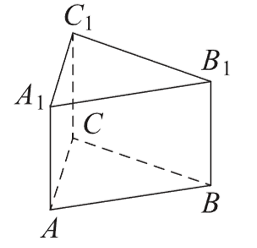
10. Найдите объём многогранника, вершинами которого являются точки C, A1, B1, C1 правильной треугольной призмы ABCA1B1C1 , площадь основания которой равна 4, а боковое ребро равно 9.
Ответ: 12

11. Найдите объём многогранника, вершинами которого являются точки A, C, A1, B1, C1 правильной треугольной призмы ABCA1B1C1. Площадь основания призмы равна 8, а боковое ребро равно 6.
Ответ: 32
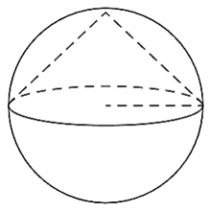
12. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 132. Найдите объём конуса.
Ответ: 33

13. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём конуса равен 47. Найдите объём шара.
Ответ: 188

14. Около конуса описана сфера. Центр сферы совпадает с центром основания конуса. Радиус сферы равен 22√2. Найдите образующую конуса.
Ответ: 44
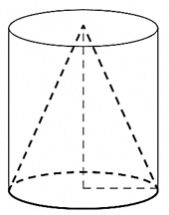
15. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 57.
Ответ: 171

16. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). объём цилиндра равен 30. Найдите объем конуса.
Ответ: 10

17. Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Причем радиус основания равен высоте. Найдите площадь боковой поверхности цилиндра, если площадь боковой поверхности конуса равна 16√2.
Ответ: 32

18. Цилиндр и конус имеют общее основание и высоту (конус вписан в цилиндр). Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 83√2. Найдите площадь боковой поверхности конуса.
Ответ: 83
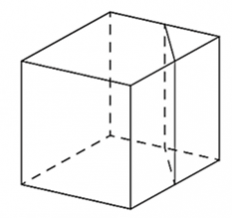
19. Объём куба равен 62. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.
Ответ: 7,75
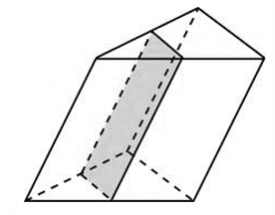
20. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.
Ответ: 16

21. Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.
Ответ: 12

22. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Ответ: 8

23. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем этой призмы, если объем отсеченной треугольной призмы равен 5.
Ответ: 20
24. Во сколько раз уменьшится объём конуса, если его высота уменьшится в 9 раз, а радиус основания останется прежним?
Ответ: 9

25. Во сколько раз уменьшится объём конуса, если радиус его основания уменьшить в 11 раз, а высоту оставить прежней?
Ответ: 121

26. Диаметр основания конуса равен 30, а длина образующей равна 39. Найдите высоту конуса.
Ответ: 36
27. В цилиндрический сосуд налили 2800 см3 воды. Уровень жидкости оказался равным 16 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 13 см. Найдите объём детали. Ответ выразите в куб. см.
Ответ: 2275
28. Даны два цилиндра. Объем первого цилиндра равен 12. У второго высота в два раза меньше, а радиус основания в три раза больше. Найдите объём второго цилиндра.
Ответ: 54
29. В цилиндрическом сосуде уровень жидкости достигает 176 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в см.
Ответ: 11
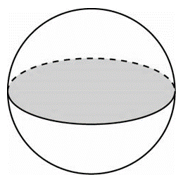
30. Площадь большого круга шара равна 3. Найдите площадь поверхности шара.
Ответ: 12

31. Площадь поверхности шара равна 78. Найдите площадь большого круга шара.
Ответ: 19,5
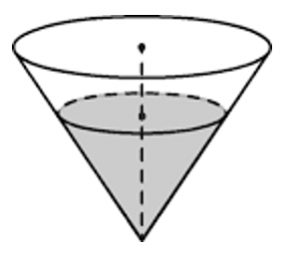
32. В сосуде, имеющем форму конуса, уровень жидкости достигает 2/3 высоты. Объём жидкости равен 16 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Ответ: 38